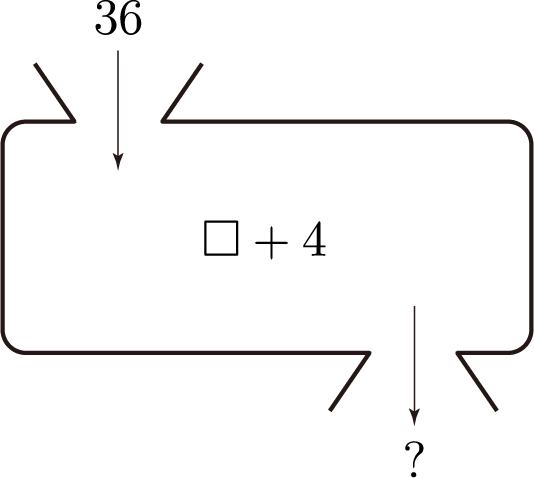
함수
덤프버전 :
분류
, 그 외에 다른 뜻에 대한 내용은 함수(동음이의어) 문서
참고하십시오.1. 개요[편집]
함수(函數, function)는 수학에서 두 집합 사이의 관계를 설명하는 논리적 개념으로, 간단하게 정의역의 원소마다 공역의 원소가 오직 하나씩 대응되는 관계를 말한다. 수학적 구조를 정의할 때는 물론 현실의 다양한 분야에서도 응용된다.
2. 정의[편집]
2.1. 교육과정 수준[편집]
중학교에서는 "[math(x)]의 값이 정해짐에 따라 [math(y)]의 값이 정해질 때, [math(y)]를 [math(x)]의 함수라고 한다."라고 설명한다. 2015 개정 이후로 함수라는 용어는 따로 쓰지 않는 듯하다.
2.2. 고등수학 수준[편집]
그 정의는 다음과 같다.
임의의 원소 [math(x\in X)]에 대해, 그에 대응하는 원소 [math(y \in Y)]가 유일하게 존재한다.[3][* 오해하기 쉽지만 이 명제의 역인 '[math(y \in Y)]에 대응하는 [math(x\in X)]'는 유일하지 않아도 된다. 짝함수, 주기함수의 예만 봐도 알 수 있다.]
- 여기서 집합 [math(X)]를 정의역(定義域, domain), [math(Y)]를 공역(共域, codomain)이라 말한다. 함수의 정의역과 공역을 강조하려면 '[math(f)]는 [math(X)]에서 [math(Y)]로의 함수(function from [math(X)] to [math(Y)])이다'는 표현을 사용하고, 보통 [math(f:X\mapsto Y)][4]라는 표기가 이를 의미한다.
- 원소 [math(x)]에 대응되는 원소를 [math(x)]의 함숫값(value of the function) 혹은 상(像, image)이라 하고, [math(f(x))][5]라 표기한다.
- 모든 함숫값들을 모은 집합을 치역(値域, image[6])이라 부르고,보통 [math(f(X))]로 표기된다.
2.3. 집합론에서[편집]
이후 집합론으로 넘어가면 함수 역시 여타 추상적인 수학적 대상들과 마찬가지로 집합 그 자체로 환원된다. 엄밀히 말해 함수는 관계, 즉 순서쌍들의 집합이다. 각 순서쌍의 왼편이 함수에 넣어지는 값, 오른쪽이 함숫값을 나타낸다. 즉, 집합론에서의 함수의 정의는 함수를 식이 아닌 값들의 대응, 즉 사상으로 바라본 것이다. 예를 들어, 함수 [math(f:\mathbb{R}\mapsto\mathbb{R})], [math(f(x)=x^2)]는 집합론에서의 정의에 따르면 이 함수의 그래프 위의 점들 [math((x,y)=(x,x^2))]의 집합 [math(f=\{(x,x^2):x\in\mathbb{R}\})] 그 자체이다. 만약 함수에 넣어지는 값이 여러 개이면 왼편은 그 값들의 순서쌍이 된다.
정의역이 [math(X)], 공역이 [math(Y)]인 함수 [math(f:X\mapsto Y)]를 조금 더 엄밀하게 정의하면 다음과 같다:
[math(f=\{(x,\,y)\mid x\in X\land y\in Y\}\;\text{s.t.}\;\forall(x,\,y)\in f\;\forall(x,\,y')\in f;\;y=y')]
[1] '선형함수'란 표현은 보통 선형 변환을 위해 남겨놓는 편이다.[2] 알파벳 f는 function(함수)의 첫글자에서 나왔다. 여러개의 함수를 나타낼 때에는 알파벳 나열하듯 [math(f, g, h, \cdots)]등의 알파벳으로 함수를 나타낸다. 물론 [math(a(x))]라거나 [math(a(b), x(f))] 등등의 형태도 함수기 때문에 낚이지 않게 주의하자. 심지어 원주율에 쓰이는 [math(\pi)]나, 숫자인 1도 함수의 이름자로 쓰이면 각각 소수 계량 함수, 집합 판별 함수라는 완전히 다른 물건이 된다.[3] [math(y)]가 유일하지 않을 경우 음함수가 되며, 엄밀히 말하면 함수가 아니다.[4] 한쪽 끝이 막혀 있는 화살표([math(\mapsto)])는 집합 사이의 관계(사상)를 나타낸다.[5] 읽기 편하라고 에프엑스라고 부르지만 영어권에서는 "function of x", 짧게는 "f of x"로 읽는다. 즉 x의 function이라는 말 그대로의 의미. fx로는 읽지 않는다. 이런 것 비슷한 것 중에 지수함수 읽는 법이 있는데, [math(a^x)] 는 "a to the power of x", 줄여서 "a to the x" 라고 읽는다. 또한 함숫값이 아니라 해석학에서는 x에 관한 함수를 지칭하는 관용적 표현의 함수 표기로도 이용된다.[6] im(f)라고 표기하는 경우가 많으나, range라고 부르기도 한다. 더러는 이미지와 레인지 두 용어를 각각 치역과 공역을 가리키는 의미로 따로 써먹기도 한다.
[7]
쉽게 말해 하나의 [math(x\in X)]값이 하나의 함숫값 [math(y\in Y)]만 가지도록 강제하는 조건이다.
이 함수에 속한 순서쌍들의 왼쪽 값만 모두 모은 집합 [math(X=\{x\mid(x,\,y)\in f\})]를 함수의 정의역, 오른쪽 값만 모두 모은 집합 [math(R=\{y\mid(x,\,y)\in f\})]를 함수의 치역이라고 한다. 이 정의를 이용해 함수 합성의 교환법칙과 결합법칙도 증명할 수 있다.
여기에 공역의 정의까지 추가해 더 엄밀한 정의를 만들 수 있다. 앞서 정의한 순서쌍들의 집합을 [math(P)]라고 할 때, [math(Y\supset R)]을 만족하는 공역 [math(Y)]를 추가하면
즉, 이 정의에 따르면 정의역과 그에 대응하는 모든 순서쌍이 같다고 해도 공역이 다르면 엄밀히 말하자면 다른 함수인 것이다. 공리적 집합론을 공부했다면 이 정의는 (공리적) 집합이 아닌 것들에 함수를 주는 일을 방지하기 위한 안전장치로 볼 수 있고, 즉 ZFC 공리계 같은 걸 진지하게 파고들지 않는 이상은 일상생활에서까지 이렇게까지 할 필요는 없다.
3. 일반인이 생각하는 함수[편집]
보통 함수 하면 실수 집합(의 부분집합)을 정의역과 공역으로 갖는 실함수를 떠올리고, 이는 실생활에서 기대하는 함수의 역할인 한 변수에 대한 다른 변수의 변화의 기술에 사용된다. 역사적으로 함수는 미적분학의 주 목적인 시간에 따른 물체 위치의 변화를 기술하면서 따라나왔다. 이것이 단순히 시간적 변화뿐만이 아니라 관련있는 숫자 둘로 일반화된 것으로 볼 수 있다. 과학에서 나오는 법칙이라고 이름 붙은 것들 대부분은 따지고 보면 뭐가 변할 때 다른 하나가 변하는 함수의 형태로 나온다는 것을 관찰할 수 있다. 비단 과학법칙이 아니라도 연관있어 보이는 두 변수가 함수로 연관되어 있다고 생각하고, 그 함수를 식으로 나타내어 결과나 경향을 예측하는 것이 함수의 주된 쓰임 중 하나인 모델링이다. 이 함수의 증감추세를 그림으로 한눈에 표현하는 그래프는 덤이다. 이런 상황에선 [math(x)], [math(y)]를 각각 독립변수(獨立變數, independent variable), 종속변수(從屬變數, dependent variable)라 부르는 경우가 많다. 흔히 말하는 '다변수함수'도 독립변수와 종속변수가 실수 여러 개로 늘어났다는 거 말고는 여기서 크게 벗어나지 않는다.
함수는 자연현상의 인과관계를 설명할 때 적합하다. 모든 현상(X)은 반드시 그에 따른 결과(Y)가 발생한다. 계속 똑같은 원인이 생기면 당연히 결과도 똑같으며, 뜬금없이 전혀 다른 결과가 생기는 경우는 없다. 컵 속 물을 예로 들자면, 우리가 일상생활에서 -30도에서 200도(정의역)까지 물의 온도를 특정한 값(X)으로 균일하게 조절하면 물은 고체/액체/기체 상태(Y)가 된다. 여기서 생각을 단순하게 해보자. 고체도 액체도 기체도 아닌 다른 상태로 존재하는 것이 가능할까? 뭐, 압력이 낮고 일정하다면 [-30, 200]에서는 일어나지 않는다. 이 부분에서 함수의 특징 중 하나인 모든 X는 반드시 그와 짝을 이루는 Y값이 있다라는 개념이 들어간다. 또 하나 생각해볼 게 있다. 임계 압력 이하에서[8] 과연 특정 온도의 물이 한 번에 두 가지 상태를 다 가지는 일이 있을 수 있을까? 상식적으로 생각해봐도 물은 액체이면 액체, 기체이면 기체여야 하며 액체이면서 기체인 경우는 말이 안 된다. 여기에 모든 X는 반드시 Y에 하나만 대응한다라는 개념이 포함되는 것이다.
물론 위의 문단은 예시일 뿐, 양자역학적 관점으로는 틀린 말이 된다. 불확정성 원리에 따르면 같은 사람이 던진 주사위라도 항상 같은 수가 나오지 않듯이 같은 조건(x)에서도 다른 결론(y)이 도출될 수 있다고 한다. 즉, '집합 [math(X)]의 원소 하나에는 [math(Y)]의 원소 하나만이 대응된다'라는 정의를 위반한 셈. 그리고 사실 액체이면서 기체, 기체이면서 액체인 경우는 존재하긴 한다. 일상생활에서는 보기 힘들 뿐, 애초에 함수 개념이 처음 제시된 때는 아직 양자역학이 들어서기 훨씬 전으로 한창 고전물리학이 태동하던 시기였단 걸 고려하자. 후술하겠지만 이러한 유형의 함수는 좀 더 넓은 의미의 함수와 관계되어 있다.
하지만 이렇게만 함수를 생각하며 고등수학의 정의를 보면 적잖은 괴리감을 느낄 것이다. 일반적인 함수는 정의역과 공역이 수의 집합일 필요도 없고, 따라서 그래프는커녕 '변수'니 '변화'니 하는 말부터 의미가 없다. 현대적인 함수의 정의는 수학자 디리클레 혹은 데데킨트의 정의[9]로, 굳이 식이니 변화니 하는 부분을 다 쳐내고 저렇게 추상적인 부분만 남긴 이유는 수학 중 해석학의 발전에 따른 수학자 수요가 일차적 원인이다. 간단히 말하면 식이나 변화(미분)의 요소가 없는 함수도 같이 생각을 해주는 게 더 일관성이 있었다. 자세한 이야기는 아래의 '함수의 역사' 부분에 서술.
물론 해석학 하나 때문에 저렇게 바꾼 건 아니다. 함수의 추상적 정의는 해석학 밖에 수학 여러 분야에서도 수가 포함되지 않는 광범위한 개념들을 함수로 편입시키며 큰 영향을 끼쳤다. 대학수학 정도만 가도 '함수의 공간'에서 '함수의 공간'으로의 '함수'[10]와 이상해 보이는 함수들이 마구 튀어나오는데, 익숙해지면 생각보다 유용하게 써먹을 곳이 많다. 일상생활과 관련이 많은 이산수학에서도 알고리즘, 관계, 분류 등을 생각할 때 여기저기서 튀어나온다. 프로그래밍 언어의 함수도 따지고 보면 여기서 비롯되었다.
4. 기본적(집합론적) 성질[편집]
4.1. 함수의 전사와 단사[편집]
- [math(f(a)=f(b) \Rightarrow a=b)] : 단사(單射, injective) 또는 일대일이라 하고 일대일인 함수를 단사함수 또는 일대일함수이라 한다.
함수가 일대일 함수임을 보일 때는 정의를 사용하기도 하지만, 명제의 대우로 [math(a\ne b \Rightarrow f(a) \ne f(b))]를 사용하기도 한다.
- [math(\forall y\in Y,\exists x\in X, f(x)=y)]. 즉 치역과 공역이 같을 때를 전사(全射, surjective) 또는 ([math(X)]에서) [math(Y)] 위로(onto)의 함수라 한다. 전사인 함수를 전사함수이라 한다.[11]
- [math(f:X\mapsto Y)]가 전사이고 단사일 때 [math(f)]를 전단사(全單射, bijective)라 한다. 전단사인 함수를 전단사함수 또는 일대일 대응(one-to-one correspondence)이라 한다. one-to-one & onto라고도 많이 사용한다.
쉽게 말하자면, 공역의 원소들 모두가 각자 대응하는 정의역의 원소들을 갖는(즉 공역과 치역이 동일한) 함수는 전사함수, 치역의 원소들 모두가 정의역의 원소들 중에서 오직 하나씩만 대응하는 함수는 단사함수라고 보면 된다.
4.1.1. 일대일대응[편집]
연속함수가 아닌 경우 꼭 증가함수 또는 감소함수가 아니어도 일대일대응이 될 수 있다. 예를 들어 집합 [math(X=\{1,\,2,\,3\})]에 대하여 [math(f:\;X\rightarrow X)]가 [math(f(1)=2)], [math(f(2)=3)], [math(f(3)=1)]로 정의된다면 증가함수도 감소함수도 아니지만 엄연한 일대일대응이다. 그래서 역함수 [math(f^{-1}(x))]도 [math(f^{-1}(1)=3)], [math(f^{-1}(2)=1)], [math(f^{-1}(3)=2)]와 같이 충분히 잘 정의된다.
또한 연속함수이고 증가함수 또는 감소함수가 아니면서도 일대일대응이 될 수도 있다. 유리함수가 대표적인 예로, [math(y=1/x)]의 경우 실수 전체의 집합에서 연속이지만 자기 자신이 다시금 역함수가 된다. 즉, 일대일대응이다. 그러나 [math(y=1/x)]은 증가함수도 아니고 감소함수도 아니다. 이처럼 특정 점에서 발산하는 경우 이와 같은 일이 가능하다.
접선의 기울기가 0인 점이 존재하지 않아야만 일대일대응인 것은 아님에 유의해야 한다. 접선의 기울기가 0인 점이라고 해서 꼭 감소하다가 증가하거나 증가하다가 감소하는 것이 아니기 때문이다. 예를 들어 [math(y=x^3)]은 [math(x=0)]에서의 접선의 기울기가 0이지만 틀림없이 증가함수이며, 따라서 일대일대응이다. 대신 이 경우 역함수의 도함수는 해당 점이 특이점이 된다.(즉, 기울기가 발산한다) [math(y=x^3)]의 역함수의 도함수
그러나 미분가능한 함수의 그래프에 접선의 기울기가 0인 점이 존재하지 않으면 무조건 일대일대응이다. 우선, 일대일대응이 되지 않으려면 증가하다가 감소하거나, 감소하다가 증가해야 한다. 그러기 위해서 함수 [math(f(x))]의 그래프는 증가하다가 감소하거나 감소하다가 증가하는 부분에서 접선의 기울기가 어느 한 순간 반드시 0이 되어야만 한다. 그런데 어떤 함수의 그래프에 접선의 기울기가 0인 점이 존재하지 않으면 그 함수는 증가하다가 감소하거나 감소하다가 증가할 여지 자체가 없어지고, 이는 곧 함수 [math(f(x))]가 일대일대응이 될 수밖에 없다는 뜻이다.
결국 '접선의 기울기가 0인 점이 존재하지 않는다'는 '일대일대응이다'의 충분조건일 뿐이지, 결코 필요충분조건은 아니다. 다시 말해서 이 두 진술을 완전히 같은 의미로 받아들여 서로 치환할 수는 없는 노릇이다.
그래프상에서 일대일대응을 확인하는 방법은 상수함수와의 교점을 이용하는 것이다. 일대일대응인 경우, 상수함수와의 교점은 반드시 1개이다. 이를 수평선 판정법(horizontal line test)이라고 한다.
4.2. 합성함수[편집]
 자세한 내용은 합성함수 문서를 참고하십시오.
자세한 내용은 합성함수 문서를 참고하십시오. 合成函數 / function composition
4.3. 항등함수[편집]
 자세한 내용은 항등함수 문서를 참고하십시오.
자세한 내용은 항등함수 문서를 참고하십시오. 恒等函數 / identity function
4.4. 역함수[편집]
 자세한 내용은 역함수 문서를 참고하십시오.
자세한 내용은 역함수 문서를 참고하십시오. 逆函數 / inverse function
4.5. 연속함수[편집]
 자세한 내용은 연속함수 문서를 참고하십시오.
자세한 내용은 연속함수 문서를 참고하십시오. 連續函數 / continuous function
5. 실함수[편집]
實函數 / real-valued function
우리가 보통 생각하는 함수로, 실수집합의 부분집합을 정의역으로 하고, 실수집합을 공역으로 하는 함수이다. 더욱 엄밀하게 표현한다면 '정의역이 실수인 실가함수'라 할 수 있는데 특히 정의역이 실수이지만 공역이 복소수인 경우(complex-valued function)와 구별하기 위해 이 용어를 사용한다.
많은 경우에는 함수가 수식으로만 주어진 경우가 많은데, 이럴 경우에는 함수가 식을 만족시키며 정의될 수 있는 최대의 영역인 '자연스러운 정의역'(natural domain)을 정의역으로 생각한다. 다항함수, 삼각함수 같으면 자연스러운 정의역은 실수집합 전체겠지만, [math(f(x)=\sqrt{x})]의 자연스러운 정의역은 [math(x\ge 0)] 정도로 간주될 수 있다. 별다른 언급이 없으면 정의역은 이 자연스러운 정의역으로, 공역은 실수집합으로 간주한다. 물론 정의역으로 어떤 부분집합을 생각해도 문제는 없다.
때때로 정의역의 다른 부분에서 다른 식을 사용함으로써 함수를 묘사하는 경우가 있는데, 이를 '조각적 정의'(piecewise definition)라 부르기도 한다. 한 예로 절댓값 함수는 다음처럼 조각적으로 정의될 수 있다.
[math(|x|=\begin{cases}x&\text{if}\ x\ge 0\\-x&\text{if}\ x<0\end{cases})]
[8] 물이 374°C, 22.1MPa인 경우 액체이면서 기체인 상태, 즉 초임계유체가 되어 버리므로 아래 문장이 성립하지 않는다.[9] 데데킨트는 영문 위키피디아에 따르면 장 디외도네(Jean Dieudonné)가 데데킨트의 1888년 논평인 'Was sind und was sollen die Zahlen?'의 한 구절을 확인한 부분이 있다. 사실 대부분 디리클레/로바체프스키가 함수의 정의 고안자로 인정받지만, 이들이 각각 1834, 1837년에 한 서술이 정확한 '정의'의 공식화인지 여부는 논란이 있다.[10] 즉 실함수를 집어넣어서 실함수가 나오는 (추상적) 함수이다. 작용소(operator)라 부르는 이 개념은 미분방정식이나 푸리에 해석을 공부할 때 등장한다.[11] 전사와 전사함수라는 표현은 현재 교육과정에서 정식으로 배우지는 않지만, 문제에는 나오니 기억해두자. [12] 배타적 논리합(XOR)이다.[13] '실수 전체의 집합에서'라는 단서를 달아야만 한다. 그렇지 않으면 그 어떤 함수에서도 최솟값, 최댓값, 극값이 존재하도록 하는 유한한 범위를 얼마든지 정할 수 있기 때문이다.
이 방정식의 우변은 함수가 [math(x\geq 0)]이면 [math(x)], [math(x<0)]이면 [math(-x)]임을 의미한다. 이렇게 정의되는 함수를 조각적으로 정의된 함수(piecewise-defined function)라 부르기도 한다. 이러한 조각적 정의 함수는 부호 함수 [math(\mathrm{sgn}(x))], 디리클레 함수 [math(\bold{1}_{\mathbb{Q}}(x))] 등이 존재한다.
이름답게 실해석학의 주요 대상이다.
5.1. 그래프[편집]
만약 [math(f)]가 정의역이 [math(D)]인 함수라면, [math(f)]의 그래프는 [math(\{(x,\ f(x))\ |\ x\in D\})]이다. 그래프는 일반적인 함수에 대해서도 정의되긴 하지만(사실 위의 함수의 집합론적 정의에서는 이 '그래프' 자체가 함수의 정의이다) 보통은 실함수에 대해서 주로 생각한다. 실함수의 경우는 정의역과 공역이 실수이므로 그 그래프는 곱집합 [math(\mathbb{R}\times\mathbb{R})], 즉 평면의 부분집합으로 나타낼 수 있다.
예를 들어 함수 [math(f(x)=x+2)]의 그래프는 [math(y=x+2)]인 점 [math((x,\ y))]들의 집합이다. 아래 그림에서 [math(x=0)]인 점을 [math(\boldsymbol y)]절편, [math(f(x)=y=0)]인 점을 [math(\boldsymbol x)]절편이라고 한다.[14]
좌표 평면의 [math(x)]축을 독립변수로 하고 각각의 [math(x)]값에 대응하는 [math(y)]값으로 수많은 점 [math((x,y))]을 찍어 선으로 연결하면 그래프를 만들 수 있는데, 이런 식으로 좌표평면 위에서 만들어지는 도형들에 대해 연구하는 학문이 해석기하학이다. [math(y=ax+b)] 꼴의 함수로 그래프를 그리면 직선이 되고, [math(y=(x-a)^2+b)]는 포물선, [math((x-a)^2+(y-b)^2=r^2)]는 원이 되는 식. 물론 초등적인 의미에서 원은 함수가 아니다. [math(x^2+y^2=1)]이라는 원의 방정식에 대해 [math(x={1\over 2})] 에 대응하는 값이 두 개가 나오기 때문. 이에 대해서는 보통 다음 음함수(implicit function)의 개념을 통해 함수로 이해하게 된다.
5.1.1. 양함수와 음함수[편집]
양함수(陽函數, explicit function) 는 우리가 원래 알고 있는 꼴인 [math(y=f(x))]가 맞다. 종속변수를 독립변수에 대하여 표현한 것이다. 이 함수가 우리가 보고 이해하기 쉬운 꼴이다. 함수에 대한 정보가 꼴을 보면 바로바로 튀어나오기 때문이다.
음함수(陰函數, implicit function)는 [math(f(x,y)=0)] 꼴로 정리되는 [math(x,y)]에 대한 모든 식을 말한다. 알다시피 이런 꼴로 정리 되는 유명한 방정식인 원의 방정식은 함수가 아니다. [math(x^2+y^2-1=0)]을 생각해보면 [math(x={1\over 2})]에 대응하는 값이 두 개가 나오기 때문에 일반적인 함수는 아니다. 그러나 저 방정식은 [math(y=\sqrt{1-x^2})]과 [math(y=-\sqrt{1-x^2})]의 두 개 함수를 은연 중에 포함하고 있다. 그래서 저러한 형태의 함수를 음함수라고 부르는 것이다.
주어진 식이 함수인지 아닌지 판단하는 방법은 정의역에 속하는 임의의 [math(x)]값에 오직 하나의 [math(y)]값의 대응하는지 확인하면 된다.[15][16]
5.1.2. 닮은꼴 함수[편집]
 자세한 내용은 닮은꼴 함수 문서를 참고하십시오.
자세한 내용은 닮은꼴 함수 문서를 참고하십시오. 함수들 중에는 그래프만으로는 구별이 어려운 함수들이 있다.
5.2. 감소, 증가 함수[편집]
증가, 감소 함수의 정의가 [math(x_1<x_2)]인 구간 [math(I)]의 모든 쌍 [math(x_1,\ x_2)]에 대해서 만족되어야 한다는 것을 아는 것이 중요하다. 구간 [math(I)]는 유한할 수도, 무한할 수도 있다.[math(f)]가 구간 [math(I)]에서 정의된 함수이고 [math(x_1,\ x_2)]가 [math(I)]의 임의의 두 점이라고 하자.
1. 만약 [math(x_1<x_2)]일 때 [math(f(x_1) \le f(x_2))]이면 함수 [math(f)]는 [math(I)]에서 증가 혹은 단조증가한다고 말한다. 만약 [math(f(x_1) < f(x_2))]가 만족된다면 강증가라고 말한다.
1. 만약 [math(x_1<x_2)]일 때 [math(f(x_1) \ge f(x_2))]이면 함수 [math(f)]는 [math(I)]에서 감소 혹은 단조감소한다고 말한다. 만약 [math(f(x_1) > f(x_2))]가 만족된다면 강감소라고 말한다.
5.2.1. 오목·볼록[편집]
 자세한 내용은 볼록함수 문서를 참고하십시오.
자세한 내용은 볼록함수 문서를 참고하십시오. 5.3. 짝함수/홀함수[편집]
 자세한 내용은 대칭함수 문서를 참고하십시오.
자세한 내용은 대칭함수 문서를 참고하십시오. 偶函數, 奇函數 / even, odd function
5.4. 주기함수[편집]
週期函數 / periodic function
함숫값이 일정 주기로 반복되는 함수. 기본적으로 전단사가 아니기 때문에 역함수를 만들기 위해서는 정의역을 주기 길이로 잘라내야 한다.[17] 가령 위의 사인함수의 역함수 [math(\arcsin(x))]는 함숫값이 [math([-{\pi}/{2},\,{\pi}/{2}])]가 되고 이로 인해 정의역이 [math([-1,1])]이 된다.
주기 함수의 정의가 교재에 따라 조금씩 다른데, [math(f(x+p)=f(x))]인 양수 [math(p)]가 존재할 때 주기함수로 정의하는 경우와, [math(f(x+p)=f(x))]인 [math(p)]인 최소의 양수 [math(p)]가 존재할 때 주기함수로 정의하는 경우가 있다. 첫 번째 경우는 상수함수나 [math({\bf 1}_{\mathbb Q})]같은 함수가 주기함수로 인정되는 반면, 뒤의 정의에서는 주기가 존재하지 않는 함수는 주기함수로 인정되지 않는다.
5.5. 실함수의 종류[편집]
5.5.1. 일차함수[18][편집]
一次函數 / linear function
상수 [math(m)]와 [math(b)]에 대하여 [math(f(x)=mx+b)]형태의 함수를 일차함수라고 부른다. [math(b=0)]일 때 함수 [math(f(x)=mx)]는 원점을 지나고 특히 [math(m=1)]일 때 함수 [math(f(x)=x)]를 항등함수라고 부른다. [math(m=0)]일 때는 상수함수라고 부른다. 그리고 원점을 지나고 기울기가 양수인 일차함수를 비례 관계라고 부른다.
한 변수가 항상 다른 한 변수의 상수배라면, 즉 0이 아닌 상수 [math(k)]에 대하여 [math(y=kx)]라면, 두 변수 [math(y,\ x)]가 비례한다고 말한다.
만약 변수 [math(y)]가 [math(1/x)]에 비례하면 [math(y)]는 [math(x)]에 반비례한다고 말한다.
선형대수학은 이 일차함수를 집중적으로 연구하는 학문이다.
5.5.2. 멱함수[편집]
冪函數 / power function
[math(a\in\mathbb R)]인 [math(a)]가 상수일 때, 함수 [math(f(x)=x^a)]를 멱함수라고 부른다. 대표적으로 다음과 같은 경우가 있다.
- [math(a=n)](양의 정수)일 때
함수 [math(f(x)=x^n)]는 모든 실수에 대하여 정의되고 [math(n)]이 커질수록 구간 [math((-1,\ 1))]에서는 [math(x)]축에 점점 가까워지고 나중에는 거의 달라붙는다. [math(|x|>1)]에서는 더 가파르게 증가한다. 항상 [math((1,\ 1))]과 원점을 지난다.
- 짝수 차수 함수는 [math((-\infty,\ 0])]에서 감소하고 [math([0,\ \infty))]에서 증가한다.
- 홀수 차수 함수는 [math((-\infty,\ \infty))]에서 증가한다.
- [math(a=-n)](음의 정수)일 때
함수 [math(f(x)=x^{-1}=\dfrac{1}{x})], [math(f(x)=x^{-2}=\dfrac{1}{x^2})], ...는 0으로 나눌 수 없으므로 [math(x \neq 0)]인 모든 [math(x)]에서 정의된다. 원점에서 멀어질수록 축에 점점 가까워진다.
- [math(n)]이 홀수일 때 [math(y=\dfrac{1}{x^n})]의 그래프는 원점에 대하여 대칭이고 [math((-\infty,\ 0),\ (0,\ \infty))]에서 감소한다. 특히 [math(n=1)]일 때의 그래프는 쌍곡선 [math(xy=1)]이다.
- [math(n)]이 짝수일 때 [math(y=\dfrac{1}{x^n})]의 그래프는 [math(y)]축에 대하여 대칭이고 [math((-\infty,\ 0))]에서는 증가, [math((0,\ \infty))]에서는 감소한다.
- [math(a=\dfrac{1}{n})](양의 정수의 역수)일 때
함수 [math(\displaystyle f(x)=x^{\frac{1}{n}}=\sqrt[n]{x})]는 거듭제곱근 함수이다. 특히 함수 [math(\displaystyle f(x)=x^{\frac{1}{2}}=\sqrt{x},\ g(x)=x^{\frac{1}{3}}=\sqrt[3]{x})]는 제곱근 함수와 세제곱근 함수이다.
- [math(n)]이 짝수일 때의 정의역은 [math([0,\ \infty))]이다.
- [math(n)]이 홀수일 때의 정의역은 [math((-\infty,\ \infty))]이다.
- [math(a=\dfrac{m}{n})](양의 유리수)일 때
위의 [math(a=\dfrac{1}{n})](양의 정수의 역수)일 때와 개형이 비슷하다.
- [math(a=-\dfrac{m}{n})](음의 유리수)일 때
위의 [math(a=-n)](음의 정수)일 때와 개형이 비슷하나, 정의역이 [math((0,\ \infty))]인 것이 차이이다.
- [math(a\notin\mathbb Q)](무리수)일 때
위의 [math(a=n,\,a=-n)]과 비슷하나, 공역이 다음과 같은 차이가 생긴다.
- [math(x\ge 0)]일 경우는 실함수이다.
- [math(x<0)]일 경우는 복소함수이다.
- [math(a<0)]일 경우, [math(\Re(f(x)))]와 [math(\Im(f(x)))]는 [math(x)]축에 대칭이다.
5.5.3. 다항함수[편집]
 자세한 내용은 다항함수 문서를 참고하십시오.
자세한 내용은 다항함수 문서를 참고하십시오. 多項函數 / polynomials
음이 아닌 정수 [math(n)]과 실수 [math(a_0,\ a_1,\ a_2,\ \dots\ a_n)](다항식의 계수라고 부른다.)에 대하여 함수 [math(p(x)=a_nx^n+a_{n-1}x^{n-1}+\ \cdots\ +a_1x+a_0)]를 다항함수라 한다. 모든 다항함수는 [math((-\infty,\ \infty))]를 정의역으로 가진다. [math(n>0)]이고 [math(a_n\neq 0)]일 때 [math(n)]을 다항식의 최고차수라고 한다. 기울기가 0이 아닌 일차함수는 차수가 1인 다항함수이다. 모든 다항함수는 연속이며 미분가능하다.
중학교 3학년에서 [math(x^2)], 즉 2차 함수가 처음 등장하며, 3차 함수는 고등학교 1학년[19], 4차 함수는 고등학교 2학년[20]부터 나오기 시작한다.
5.5.4. 이산함수[편집]
離散函數 / discrete function
함숫값의 집합이 연속이 아닌 함수를 뜻한다. 연속이 아니므로 미분이 불가능하기 때문에 해석학이나 미적분학에서는 다뤄지지 않다시피 하지만, 정수론이나 이산수학에서는 비중있게 다뤄진다. 이산함수 중 값이 정체되어 있다가 일정 주기로 증가하는 함수는 따로 계단 함수(Step Function)로 일컫기도 한다.
대표적인 이산함수로 소수 계량 함수가 있다.
5.5.4.1. 산술함수[편집]
 자세한 내용은 산술함수 문서를 참고하십시오.
자세한 내용은 산술함수 문서를 참고하십시오. 算術函數 / arithmetic function
이산함수 중, 정수론적인 쓰임이 많은 함수들을 이른다.
5.5.5. 논리함수[편집]
 자세한 내용은 논리함수 문서를 참고하십시오.
자세한 내용은 논리함수 문서를 참고하십시오. 論理函數 / boolean function
함숫값이 단 두 개로 나타나는 함수를 이른다.
5.5.6. 병리적 함수[편집]
 자세한 내용은 병리적 함수 문서를 참고하십시오.
자세한 내용은 병리적 함수 문서를 참고하십시오. 病理的 函數 / pathological function
여느 함수와는 동떨어진 특성[21]을 띠는 함수를 뜻한다.
5.5.7. 분포[편집]
分布 / distribution
시험 함수(test function)의 도움을 받아야만 정의할 수 있는, 함수보다 느슨한 형태의 해석학적 대상을 이른다.
대표적으로 디랙 델타 함수가 있다.
5.5.8. 일변수 함수의 극한[편집]
 자세한 내용은 극한 문서를 참고하십시오.
자세한 내용은 극한 문서를 참고하십시오. 6. 복소함수[편집]
複素函數 / function of a complex variable
정의역이나 공역, 또는 둘 모두가 복소수인 함수. 복소수가 반쌍형성을 갖기 때문에 연속과 미분가능성의 조건이 실함수에 비해 매우 엄격하지만 미분 가능함이 곧 연속함수이자 해석함수가 되는 깔끔한 성질을 띤다는 점이 있다. 이런 함수를 다루는 학문이 복소해석학이다.
7. 다변수 함수[편집]
 자세한 내용은 다변수함수 문서를 참고하십시오.
자세한 내용은 다변수함수 문서를 참고하십시오. 多變數函數 / function of several variables
함수는 위에서 말했듯이 집합 [math(X)]의 각 원소 [math(x)]에 집합 [math(Y)]의 원소 [math(y)]가 오직 하나만 대응할 때 [math(X)]에서 [math(Y)]로의 함수라고 한다. 그리고 집합 [math(X)]는 정의역이라 하고 집합 [math(Y)]는 공역이라 한다. 여기서 [math(X)]의 원소들의 상의 집합 [math(\{f(x)|x\in X\})]는 [math(Y)]의 부분집합으로 치역이라 한다. 이때 [math(x)]를 독립변수라 하고 [math(y)]를 종속변수라 한다. 여기서 일변수 함수인지 이변수 함수인지 판별하는 것은 간단히 독립 변수의 개수이다. 독립변수가 1개면 일변수 함수, 2개면 이변수 함수, n개면 n변수 함수, 변수가 무한히 많으면 무한 다변수 함수이다.
대표적인 다변수 함수로 초기하함수가 있다.
7.1. 이변수 함수[편집]
二變數函數 / functions of two variables
이변수 함수는 말 그대로 독립변수가 2개인 함수이다. 일변수 함수와 다르게 꼴이 [math(z=f(x,y))]처럼 생겼다.[22] 음함수와 헷갈리면 안 된다. 음함수는 [math(f(x,y)=0)]이다. 굳이 생각 하자면 음함수는 [math(x,y,z)]공간의 이변수 함수[math(z=f(x,y))]와 평면 [math(z=0)]의 교선이라고 생각해도 된다. 어쨌든 이변수 함수는 일변수 함수와 다르게 실수가 실수에 대응하는 게 아니라 실수의 순서쌍 [math((x,y))]이 실수에 대응하는 것이다.
여기서 [math(R)]이 함수 [math(f)]의 정의역이고 공역이 실수 집합 [math(\mathbb{R})]이다. 여기서 [math(x,y)]가 독립변수, [math(z)]가 종속변수가 된다.[math(f:R\subset\mathbb{R^2}\to\mathbb{R})]
[math(z=f(x,y))] 형태의 이변수함수는 대개 역함수를 정의할 수 없다. 왜냐하면
정의역이 [math(\mathbb{R^2})]이고 공역이 [math(\mathbb{R})]이기 때문이다. 굳이 역함수를 정의하려면
정의역이 [math(\mathbb{R^2})]이고 공역이 [math(\mathbb{R^2})]인 함수를 새로 정의해야 한다.
일변수 함수가 [math(x,y)]축이 직교하는 평면인 2차원에서 자취가 그려지는 것처럼, 이변수 함수는 [math(x,y,z)]축이 모두 직교하는 공간인 3차원에서 자취가 그려진다.
이변수 함수는 공간상에서 그려지기 때문에 울프럼알파나 지오지브라 같은 것들을 동원하지 않은 이상 그리기가 쉽지는 않다. 보통 우리는 이변수 함수의 곡면의 개형을 그릴 때는 평면상에서 등고선과 등위선으로 접근한다. [math(z)]축을 일정한 상수 [math(c)]로 고정시키면 [math(z=c)]와 [math(z=f(x,y))]의 교선이 생긴다. 이 교선을 [math(xy)] 평면에 사영한다. 여기서 교선의 사영을 등위선, 이러한 곡선의 모임을 등고선이라 한다.
그런데, 일변수 함수처럼 보이는데도 이변수 함수인 함수가 있다. 바로 복소함수. 복소함수의 정의역은 [math(\mathbb{R})]이 아니라 [math(\mathbb{C})]인데, [math(\mathbb{R}^2\to\mathbb{C})]로 대응되는 함수[23]가 존재하기 때문에, [math(\mathbb{R}^2\sim\mathbb{C})]이 될 수 있고, 따라서 틀림없이 함수가 [math(f(z))]로 변수는 [math(z)] 하나뿐인데도, [math(z=\Re(z)+i\Im(z)=x+iy)]이므로 사실상 변수가 2개인 함수인 [math(g(x,y))]로 대응시킬 수 있기 때문. 게다가 복소함수는 평범한 실함수와는 다르게, 특정 경우가 아니라면 4차원 공간에서 그려지는 함수이기 때문에, 울프럼알파나 지오지브라를 동원한다고 해도 완벽하게 그리는 건 불가능하다. 주로 이런 경우 그래프의 개형은 절댓값을 취해서 그리는 게 일반적.[24] 실제로 복소함수는 일반적으로 이렇게 표현한다. [math(f(z)=f(x+iy)=u(x,y)+iv(x,y))]
이렇게 낯설어 보이는 개념이지만, 의외로 일상생활에도 쓰는 곳이 있는데 대표적으로 반올림이 있다. 변수 하나는 반올림할 수, 다른 변수 하나는 소수점 자릿수로 생각하면 반올림이 2변수 함수라는 것을 알 수 있다.
이외에도 최대공약수, 최소공배수 등이 있다.
7.2. 동차함수[편집]
 자세한 내용은 동차함수 문서를 참고하십시오.
자세한 내용은 동차함수 문서를 참고하십시오. 同次函數 / homogeneous function
7.3. 벡터 함수, 텐서 함수[편집]
더 나아가, 함수의 정의역으로 수 집합이 아닌 벡터 공간을 받을 수 있는데 이를 벡터 함수(vector function)라고 한다. 벡터가 수의 '꾸러미'이기 때문에 일반적인 수로는 하기 복잡한 계산[25]이 필요한 곳에 쓰인다. 더 일반화하면 텐서 함수(tensor function)를 생각할 수 있다.
대표적으로 내적, 외적, 거리함수 등이 있다.
8. 해석함수[편집]
解析函數 / analytic function
모든 함숫값을 테일러 급수 같은 멱급수로 쪼갤 수 있는 함수.
당연하겠지만 해석함수가 아닌 함수도 있다. 절댓값 함수가 대표적으로, [math(x=0)]에서의 미분계수가 존재하지 않기 때문에 해석함수가 아니다.
8.1. 정칙함수[편집]
正則函數 / holomorphic function
해석함수 중에서도 연속이고 매끄러운 함수를 뜻한다. 위의 병리적 함수와 대비해서 참한 함수(well-behaved function)라고 하기도 한다.
9. 초등함수[편집]
 자세한 내용은 초등함수 문서를 참고하십시오.
자세한 내용은 초등함수 문서를 참고하십시오. 初等函數 / elementary function
다항함수, 지수함수 같이 대수학적 도구로 다룰 수 있는 함수를 뜻한다.
10. 초월함수[편집]
 자세한 내용은 초월함수 문서를 참고하십시오.
자세한 내용은 초월함수 문서를 참고하십시오. 超越函數 / transcendental function
[math(y=\sin x)], [math(\displaystyle y=\int_0^x{1\over\ln t}dt)] 같이 대수적으로 정의할 수 없는 함수들을 뜻한다. 특수함수라고도 부른다.
11. 범함수[편집]
汎函數 / functional
함수 그 자체를 정의역으로 삼는 함수이다.
12. 함자[편집]
函子 / functor
범주론에서는 집합론적 함수보다 추상화, 일반화한 개념인 사상(morphism)을 중심으로 수학적 구조를 바라본다. 이에 따라 단사함수, 전사함수, 전단사함수 등의 용어도 모닉사상(monomorphism), 에픽사상(epimorphism), 동형사상(isomorphism) 등으로 미묘하게 바뀌는데[26], 그것이 집합론적 함수를 논하며 말하는 그것과 같은듯 하면서도 미묘하게 다르다는게 함정이다.
범주론에서는 사상의 대상으로 수학적 구조, 그리고 범주 그 자체를 대상으로 삼는 것도 허용하기 때문에 집합론적인 함수 개념과는 달라진다. 예를 들어서 1<2 같은 단순한 부등호조차도 범주론에서는 1→2라는 관계가 존재한다고 보고, 이를 사상으로 취급할 수 있다. 이런 식으로 확장된 사상 중에서 두 범주 간의 사상으로서 사상끼리의 합성과 항등사상을 보존하는 것을 함자(functor)라고 부른다.
13. 함수의 역사[편집]
13.1. 함수 개념의 태동[편집]
초창기의 함수는 하나의 변수 [math(y)]가 다른 변수 [math(x)]의 변화에 어떻게 반응하는지 개념이었다. 이 개념이 등장하기 위해서는 '변수', '변화' 두 가지의 개념이 필요했다. 즉 '변수'를 만들어 낸 해석기하학과 '변화'를 생각해 낸 미적분학이 함수를 탄생시킨 부모인 셈이다.
시간순서로는 해석기하학이 좀 더 빠르게 나왔다. 데카르트가 좌표를 생각해내며 등장한 해석기하학은 (교과과정의 '도형의 방정식' 부분에서 나오듯이) 여러 가지 도형을 대수식으로 나타낼 수 있는 쓰임새가 있었지만, 어찌 보면 변수라는 개념의 등장 그 자체가 영향이 더 컸다. 이전에도 도형에 대해서 숫자를 대응시키기는 했지만 그것은 선분 사이의 길이비 정도에 국한되어 있었기 때문에 좌표는 현실의 공간을 수와 완전히 일대일대응시키는 첫걸음이었다. 곡선을 따라 움직일 때 좌표 x, y가 변한다는 것을 관찰하며 사람들은 그리스 수학에서는 금기시되었던 변화의 개념에 다가갈 수 있었다.
통념과는 다르게 미분의 전신인 무한소 해석(infinitesimal calculus)이 탄생한 것도 운동이 아니라 이 곡선의 궤적을 관찰하는 것이 먼저였던 것도 이러한 해석기하학의 발전에 근거했다. 이 무한소해석의 태동은 그때 마침 고개를 들고 있었던 적분이론과의 통합 등등을 통해 미적분학의 정립으로 나아가게 되고, 이것이 해석기하학과 다시 융합되어서 공간 속의 곡선에 대해 미적분을 하는 단계에 이르렀다. 이후에 시간에 따른 운동의 변화가 미분으로 설명된 것은 굳이 따지자면 조금 더 나중의 이야기이다.
함수의 이름, 즉 'function'이란 용어도 이때 라이프니츠에 의해 처음 고안되었다. 처음 라이프니츠의 함수의 의미는 기하학적인, 즉 곡선에서 두 변수의 연관 정도에 국한되어 있었지만, 여기에 요한 베르누이가 '식으로 나타내지는 대상'이라는 묘사를 갖다붙였다. 이것이 극단에 이르러 근대적 대수학의 이론이 상당히 발전한 오일러 대에는 "해석적 표현", 즉 테일러 급수(무한히 나가는 멱급수)로 나타낼 수 있는 것들을 함수라 이르게 된다. 물론 저 때에는 테일러 정리 정도는 기본으로 깔려 있었기 때문에 가능한 일이다. 어찌 보면 라이프니츠가 함수의 정의를 내렸다기보다는 함수라는 말에 이것저것 달라붙어서 커져 온 거에 가깝긴 하지만, 그래도 거대한 눈덩이의 시작이 되었다는 점은 체계를 잡았다는 느낌으로 충분히 높게 평가할 수 있다. 대신에 기호 [math(f(x))]를 고안한 것은 라이프니츠가 아니라 오일러였다. 라이프니츠는 [math(df/dx)]까지 쓰긴 했지만 괄호 안에 변수를 넣진 않았었던 것이다.
다만 이렇게 불어난 함수의 의미, 즉 지금의 언어로 말하자면 "함수=곡선=변화=테일러 급수"라는 관념은, 19세기부터 서서히 흔들리기 시작한다.
13.2. 해석함수에 대한 의문[편집]
해석함수 공격에 첫 단추를 끼운 것은 의외로 푸리에 해석이었다. 조제프 푸리에가 파동을 연구하면서 나온 푸리에 급수(즉 사인/코사인 함수의 무한합)에서 푸리에는 처음으로 연속이 아닌 '식'을 찾아낸다. 지금으로 비스무레하게 말하면 사각파 이런 애들을 푸리에 급수로 나타낸 것이다. 해석적인 식은 어디에서건 연속이므로[27] 푸리에 급수는 오일러의 함수 범위에선 확실히 벗어난 셈이다. 대신에 푸리에는 모든 함수는 푸리에 급수로 나타낼 수 있다는, 즉 "함수=푸리에 급수"라는 더 급진적인 주장을 해버린다. 이 때문에 푸리에 급수가 항상 원래 함수로 수렴하는지의 문제가 수학자들의 떡밥으로 떠올랐다.
디리클레는 증명을 찾으려는 수많은 수학자들을 대신해 이 떡밥을 해결하며, 항상 그렇지는 않다는 결론을 내었다. 즉 푸리에 급수마저도 함수의 정의로서는 한계가 있다는 것을 지적한다. 여기에 덧붙여 그는 다음과 같이 정의되는 디리클레 함수를 제시한다.
[math({\bold 1}_{\mathbb Q}(x)=\begin{cases}1&\text{if }x\in\mathbb{Q}\\0&\text{if }x\notin\mathbb{Q}\end{cases})]
[14] 3차원 이상에서는 좌표축의 이름에 따라 [math(z)]절편, [math(w)]절편, [math(t)]절편 같은 것들도 있다.[15] 그래프가 주어졌을 때 함수가 아닌지 판단하는 방법은 정의역에 속하는 임의의 [math(x)]값에서 [math(y)]축에 평행한 수직선이 그래프와 만나는 점이 한 개인지 확인만 해주면 된다.[16] 아까 원의 방정식은 그래프를 보기만 해도 함수가 아닌 것을 알 수 있다.[17] 복소해석학에서는 이를 분지 절단(branch cut)이라고 부른다.[18] '선형함수'란 표현은 보통 선형 변환을 위해 남겨놓는 편이다.[19] 보통 이때쯤 되면 출제되는 방정식 문제들의 실근의 절댓값이 10을 넘지 않는다는 등 요령만 잘 깨우치면 대입법으로도 3차 방정식을 어렵지 않게 풀 수 있다. 고등학교 1학년에서 출제되는 3차 방정식의 경우, 모든 항의 계수가 유리수이기 때문에, 적어도 한 개의 유리근이 나오므로 위 방법대로 1개의 근을 구하고, 나머지 두 근은 근의 공식으로 구하면 된다.[20] 이 역시 고등학교 1학년의 4차 방정식에도 적용 가능한 풀이법이며 이는 최소한 2개의 실근이 보장되며, 앞에서 말했듯이 모든 항의 계수가 유리수이고, 거기다가 극히 일부 문제를 제외한 모든 4차 방정식 문제가 난이도 조절 문제로 1로 고정되기 때문이다.[21] 모든 점에서 불연속이거나, 연속이지만 어디서든 미분이 불가능한 등[22] , 대신 ;를 쓰기도 한다.[23] [math(\mathbb{R}^2\to\mathbb{C})]:[math((a,b)\to a+bi)]
[math(\mathbb{C}\to\mathbb{R}^2)]:[math(z\in\mathbb{C},f(z)=(\Re(z),\Im(z))\text{(}\Re(z),\Im(z)\in\mathbb{R}\text{)})][24] 편각을 색도로 표현한 다색 복소평면을 쓰기도 한다. 이 경우 2차원상에서 표현이 가능하다.[25] 독립변수의 개수가 가변적일 경우가 대표적이다.[26] 선형대수학, 현대대수학을 공부해봤다면 이 용어들이 익숙할 것이다. [27] 테일러급수는 수렴반경 밖에서는 발산하기는 하지만, 불연속점이 나오는 경우는 없다.
[math(\mathbb{C}\to\mathbb{R}^2)]:[math(z\in\mathbb{C},f(z)=(\Re(z),\Im(z))\text{(}\Re(z),\Im(z)\in\mathbb{R}\text{)})][24] 편각을 색도로 표현한 다색 복소평면을 쓰기도 한다. 이 경우 2차원상에서 표현이 가능하다.[25] 독립변수의 개수가 가변적일 경우가 대표적이다.[26] 선형대수학, 현대대수학을 공부해봤다면 이 용어들이 익숙할 것이다. [27] 테일러급수는 수렴반경 밖에서는 발산하기는 하지만, 불연속점이 나오는 경우는 없다.
해석학을 배운 사람이라면, 이 함수는 어디에서도 연속이 아니라는 것을 알 수 있을 것이다. 연속뿐만 아니라 모든 구간에서 리만 적분이 존재하지 않는다. 하지만 이 함수를 표현하는 다음과 같은 식이 존재한다(...)
[math(\displaystyle {\bold 1}_{\mathbb Q}(x)=\lim_{m \to \infty}\Bigl[\lim_{n \to \infty}\cos^{2n}(m! \pi x)\Bigr] \qquad (m, n\textsf{은 자연수}))]
당시엔 엡실론-델타 판정법이 완벽하게 정립된 것은 아니었고 리만적분도 아직 정의되기 전이었지만, 그래도 이게 연속이 아니고 보통의 적분도 안되는 것 쯤은 알 수 있었다. 물론 저 극한 식은 그때에는 없었을 것이다. 디리클레는 더 나아가서 함수의 엄밀한 정의를 거의 내릴 뻔하지만, 아쉽게도 조각적인 연속함수의 개념에 그친다. 하지만 디리클레의 이 정의에는 "함수는 수학적 연산으로 나타날 필요가 없다"는 내용은 확실히 쓰여져 있다. 로바체프스키도 1834년 비슷한 서술을 한 바가 있어서[28] 디리클레와 로바체프스키를 사실상의 함수의 정의를 내린 사람들로 꼽는 사람이 많다.
근대 함수의 두 가지 요소인 '식'과 '연속' 중 '식'은 이렇게 날아갔지만, '연속'을 떼내는 데에는 시간이 조금 더 걸렸다. 다만 이것은 위의 디리클레 함수의 예시에서 보듯이, 불연속함수가 존재할 가능성을 생각을 못했다는 것보다는 이것을 함수로 인정해 줘야 하는지를 고민했던 것에 더 가까울 것이다. 이것은 코시의 뒤를 이어 바이어슈트라스가 극한의 완벽한 정의인 엡실론-델타 논법을 완성하면서, 즉 연속이 무엇인지 정확히 알게 됨으로서 해결되었다. 바이어슈트라스가 모든 점에서 연속이지만 미분 불가능한
13.3. 함수의 정의 이후[편집]
19세기 말의 데데킨트 시점까지 가면 (집합론에서의 약간의 변경을 제외하면) 우리가 현대에 쓰는 함수의 정의가 완벽히 정립된 것으로 본다. 이렇게 이제까지의 불확실성을 모두 떨어내고 함수, 극한, 연속 등을 완벽히 정의한 미적분학은 이 정의들을 바탕으로 해석학이란 이름으로 다시 태어나게 된다.
어떻게 보면 함수의 정의는 극한, 연속, 미분 등의 다른 개념들의 정의와는 다른 방향으로 변화했는데, 다른 것들은 직관적으로 보이는 것들을 엄밀하게 정의해 복잡해진 느낌이 있지만 함수의 정의는 더욱 간소화되었다는 차이가 있다. 물론 정의는 간단할수록 좋지만, 어찌 보면 정의가 간단해진만큼 함수의 범위는 더욱 넓어져서 온갖 괴상한 함수들을 데리고 와야 한다는 뜻이다.
한편 이렇게 간단해진 함수의 정의로 인해, 함수는 해석학 외의 다른 분야에서 '구조'를 정의하는 일을 맡을 수가 있었다. 사실상 군론의 시작을 연 대칭군(치환군)부터가 따지고 보면 함수들의 모임이고, 선형대수학에서 나오는 선형 변환을 생각하는 데에도 함수의 개념이 필요하다. 여기서 더 나아간 추상대수학을 배우면 초반에는 대수적 구조랑 함수놀이만 하고 있는 자신을 볼 수 있을 것이다. 위에서 단사/전사/전단사 등을 정의한 게 니콜라 부르바키였다는 것을 보면 언뜻 눈치챘겠지만, 이 함수의 정의도 부르바키식 개편에 잘 들어맞아 채택된 느낌이 있다. 애초에 디리클레의 정의를 집합론적인 정의(1.1.3의 정의)로 엄밀하게 못박은 게 부르바키라, 저 함수의 정의를 디리클레-부르바키 정의라고 부르기도 하니까... 이 부르바키식 개편의
부르바키의 집합론적 정의가 1939년에 등장하기까지에는 또 의외로 길고 긴 우여곡절이 있지만, 모두 따라가자면 수리논리학과 공리적 집합론의 발전사와 엮여 이야기가 매우 길어진다. 재미있는 것은 2번 문단의 함수 내용도 이 과정에 나름의 빚을 지고 있다는 것인데, 힐베르트가 함수를 정의하려는 과정에서 나온 불완전성 정리, 정지 문제 등과 연관되어 알고리즘과 계산가능성 이론, 결국에는 튜링 머신까지 튀어나왔기 때문이다.
14. 여담[편집]
- 함수(函數)라는 어휘는 중국에서 function을 음차한 것이다. 자주 초등/중등교육과정에서 함수는 입력값을 넣으면 입력값에 따르는 특정한 출력값이 나오는 '보이지 않는 마술상자'처럼 비유되는데, 유치해 보이는 이 관점이 외려 함수의 정의와 더욱 근접한다. 함수라는 단어는 函(상자)의 의미 또한 절묘하게 살린 번역이었다. 여담이지만 국어사전을 따른 '함수'의 표준발음법은 [함수]가 아니라 [함:쑤]다. 꽤나 많은 사람들이 간과하고 있는 사실이었으나, 2017년 12월 3일부로 표준발음이 개정되어 [함수]라고 읽는 것도 허용했다.
15. 관련 문서[편집]
- 로그함수
- 르장드르 함수
- 미지수
- 베타, 감마, 델타, 제타 함수
- 베셀 함수
- 삼각함수
- 소수 계량 함수
- 수학
- 쌍곡선함수
- 오차함수
- 이차함수
- 이항 관계
- 일차함수
- 지수함수
- 집합 판별 함수
- 초월함수
- 파동함수
- 확률 밀도 함수
- 함수(프로그래밍)
- Microsoft Excel/함수 목록
[28] 참고: 영문 위키피디아[29] 범주론에서의 사상의 정의역과 공역은 굳이 집합일 필요가 없는 임의의 오브젝트가 되기 때문에, 집합론에서의 집합과 함수로는 표현이 불가능한 정말 많은 것들의 표현이 가능해진다. 너무 많아서 문제지