부호 함수
덤프버전 :
분류
1. 개요[편집]
부호 함수(sign(um) function)[1]는 특수함수 중 하나로, 어떤 실수의 부호를 출력하는 함수이다. 쉽게 말해 [math(|x|)]를 미분한 함수. 기호로는 [math(\mathrm{sgn}\,x)]로 쓰며, 정의는 아래와 같다.
[math(\displaystyle \mathrm{sgn}\,x \equiv \begin{cases}
\displaystyle \frac{x}{|x|} & \text{ if } x \neq 0 \\
\\
0 & \text{ if } x=0
\end{cases} )]
구체적인 값은 아래와 같다.
[math(\displaystyle \mathrm{sgn}\,x=\begin{cases}
\displaystyle 1 & \text{ if } x>0 \\
\displaystyle 0 & \text{ if } x=0 \\
-1 & \text{ if } x<0
\end{cases} )]
보통 점화식에서 특정항의 부호만을 취할 때 사용되는 함수이다.
2. 성질[편집]
- 부호 함수는 멱등 함수이다. 즉,
[math( (\mathrm{sgn} \circ \mathrm{sgn})(a)=\mathrm{sgn}\, a )]
- 부호 함수는 홀함수(Odd function, 기함수)이다. 따라서
[math( \mathrm{sgn} \,x=-\mathrm{sgn}\,(-x) )]
- 계단 함수(Step function)의 일종이다. 부호 함수와 단위 계단 함수는 다음과 같은 관계가 성립한다.
[math(\dfrac{1 + \mathrm{sgn} \,x}{2}=\mathrm{u}\,(x) )]
- 비약 불연속점(Point of jump discontinuity)이 [math(x=0)]에서 존재한다. 즉,
[math( \begin{aligned} \lim_{x \to 0^{+}} \mathrm{sgn}\, x &=1 \\ \lim_{x \to 0^{-}} \mathrm{sgn}\, x &=-1 \end{aligned})]
[math( \dfrac{\mathrm{d}}{\mathrm{d}x} (\mathrm{sgn}\,x) =2 \delta (x))]
[math(\displaystyle \int \mathrm{sgn}\,x\,\mathrm{d}x=|x|+C )]
- 정의역이 복소수인 경우는 [math( \{ -1,\,0,\,1 \})]이 아닌 다른 값을 띄게 되는데, 이는 복소수의 절댓값이 실수하고는 다르게 정의[2]되기 때문이다. 다만, 원점과의 거리는 항상 1이 된다.[3]
- 절댓값이 정의된 대상이라면 그 대상이 무엇이든 부호 함수를 취할 수 있다. 벡터의 경우 [math({\bold{v}}/{\sqrt{\left< \bold{v} ,\, \bold{v}\right> }})], 행렬의 경우 [math(A/{\det{A}})] 같은 식으로 계산할 수 있다.
3. 복소 부호 함수[편집]
[math(\displaystyle \mathrm{csgn} (z) = \begin{cases} \dfrac{\Re(z)}{\|\Re(z)\|} & \mathrm{if} \ \Re(z) \neq 0 \\ \\ \dfrac{\Im(z)}{\|\Im(z)\|} & \mathrm{if} \ \Re(z) =0,\, \Im(z) \neq 0 \\ \\ 0 & \mathrm{if} \ \Re(z) = 0,\, \Im(z) = 0 \end{cases} )]
복소수에서 부호 함수가 '부호 판별'의 기능을 잃어버리기 때문에 복소수에 맞게 재정의한 함수이다.
정의를 보듯, 순허수인 경우에만 허수부의 부호를 판별하고 나머지는 실수부의 부호를 판별한다.
4. 기타[편집]
- 간단한 정의임에도 중등교육과정 이하에서 코빼기도 보이지 않는 함수이다.[4] 대학 과정에서 푸리에 변환을 배울 때 처음 접한다.
- 푸리에 변환의 결과로 나오는 함수는 분수함수이다: [math(\widehat{\rm sgn}\,x = -i/ \pi \xi)]
- 컴퓨터과학에서는 음수 값을 1, 양수 값을 0으로 정의한다는 차이점이 있다.[5] 이 정의는 헤비사이드 계단 함수와 천장함수를 사용한 [math(1 - \lceil u(x) \rceil)] 또는 집합 판별 함수을 사용한 [math(\mathbf{1}_{\mathbb{R^-}})]과 동치이다.
- 부호 함수에 [math(x)]를 곱할 경우에는 [math(x=0)]에서 미분이 불가능하지만, [math(x^2)]을 곱한 [math(x^2\operatorname{sgn}{x})]는 전 구간에서 미분이 가능하다.[6]
- Microsoft Excel에도 부호 함수가 존재한다. SIGN(number).
- 지수함수로도 정의가 가능하다: [math(\displaystyle \mathrm{sgn}\,x=\lim\limits_{n\to\infty}\frac{1-2^{-nx}}{1+2^{-nx}})]
- 행렬식을 일반화할 때 등장한다.
 이 문서의 내용 중 전체 또는 일부는 2023-12-01 05:57:23에 나무위키 부호 함수 문서에서 가져왔습니다.
이 문서의 내용 중 전체 또는 일부는 2023-12-01 05:57:23에 나무위키 부호 함수 문서에서 가져왔습니다.[4] 정작 수학Ⅱ의 함수의 극한, 함수의 연속 파트에서 부호 함수를 알아야 풀 수 있는 문제가 출제되곤 한다.[5] 정의하는 위치는 MSB(Most Significant Bit), 즉 맨 왼쪽 자리다. 2진법에서는 음수를 보수로 바꿔서 처리하기 때문에 음수는 가장 앞 자리(왼쪽 자리)가 1이 되기 때문.[6] 실제로 부호함수에 [math(x)]를 곱하면 [math(|x|)] 함수가 되며 , [math(x^2)]을 곱하면 [math(x|x|)] 함수가 된다. 그 후 0에서 양쪽의 미분계수를 구해보면 된다.

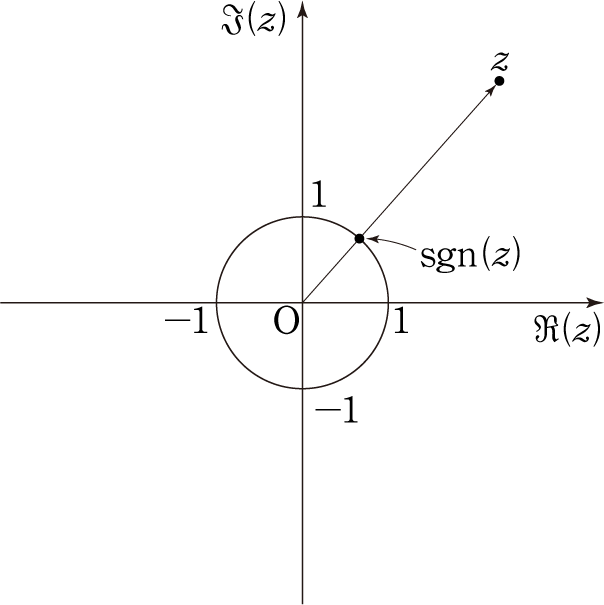 위 그림과 같이 복소평면 상 복소수 [math(z)]에 대한 부호함숫값 [math({\rm sgn} \, z)]는 복소평면 상 상에 존재한다.
위 그림과 같이 복소평면 상 복소수 [math(z)]에 대한 부호함숫값 [math({\rm sgn} \, z)]는 복소평면 상 상에 존재한다.